Determining the temperature profile of an atmosphere is a difficult subject. As a first approximation brightness temperatures derived from different wavelengths can be assigned to the depths from which they arise. A rigorous approach however requires sounding measurements from as many atmospheric levels as possible. The most basic technique involves find the pressure level where a spectral band achieves unit optical depth and then assigning the band brightness temperature to that level. As figure 3 shows however, the contribution at a particular wavelength can be spread across many pressure levels.
There are three distinct methods of temperature inversion, comparing
the measured radiance to the atmospheric model using radiative
transfer as a filter, fitting atmospheric models to the measurements,
and using an inversion algorithm to retrieve the atmospheric profile
directly using the observations (Hanel et al. 1992). The latter
choice is the one I will adopt. It consists
of solving the radiative transfer equation simultaneously for each
wavelength band giving a vertical profile of B
(T) which can
then be solved for the temperature. The most popular technique for
this is a non-linear weighted relaxation method developed by
Chahine (1972) that iterates on computed intensities until they match with
the observations. Inherently though, temperature
inversion is very dependent upon the model used as the best
measurements only break the atmosphere down into a P vs. T/
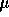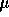profile. It will be very important to obtain the best profile of
atmospheric constituents possible.